In the quest for efficient quantum error correction methods, Hayato Goto from the RIKEN Center for Quantum Computing in Japan has introduced a novel approach known as “many-hypercube codes.” This technique aims to address the scalability issues associated with traditional quantum error correction methods, paving the way for fault-tolerant quantum computing.
Traditionally, quantum error correction involves encoding a single logical qubit onto multiple entangled physical qubits and using a decoder to retrieve the logical qubit. However, this approach suffers from scalability issues, as the number of physical qubits required increases significantly, leading to resource overheads. To overcome this challenge, high-rate quantum codes, such as quantum low-density parity-check codes, have been explored. Despite their potential, these codes require sequential setup of logical gates, resulting in less efficient time utilization.
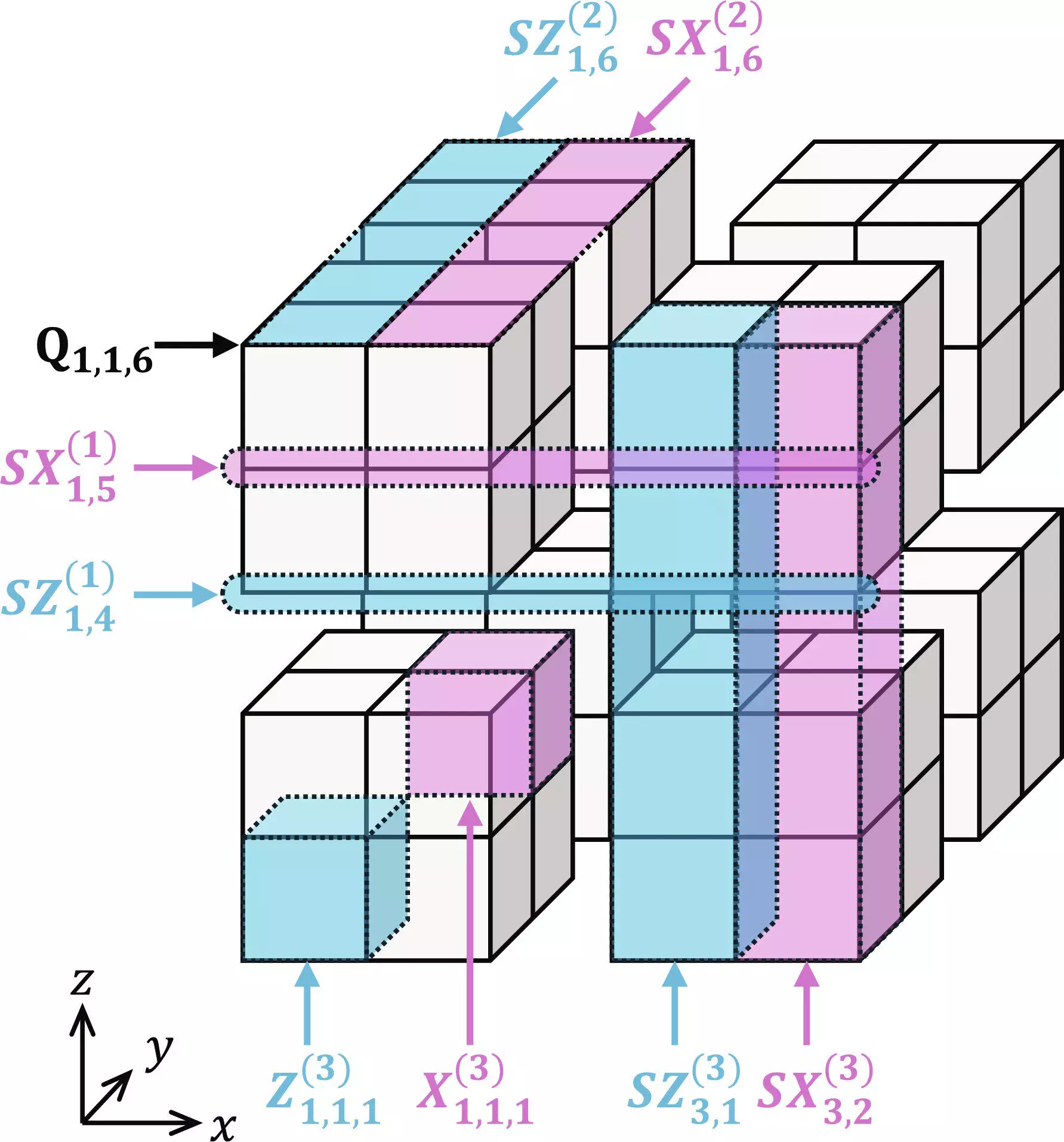
Goto’s innovative approach, termed “many-hypercube codes,” introduces a new method called high-rate concatenated quantum codes. This method visualizes logical qubits as forming a “hypercube,” a complex geometric shape that includes squares, cubes, and higher-order structures like the tesseract. The unique mathematical and geometric properties of the code set it apart from traditional high-rate quantum codes, which often have intricate structures.
To enhance the performance of the many-hypercube codes, Goto developed a dedicated decoder based on level-by-level minimum distance decoding. This technique enables high performance and allows for parallel implementation of logical gates, similar to parallel processing in classical computers. Goto describes this approach as “high-performance fault tolerant computing,” drawing an analogy to “high-performance computing” used in massively parallel computing scenarios.
The development of many-hypercube codes has yielded promising results, with encoding rates of up to 30% achieved, making them potentially the world’s highest among fault-tolerant quantum computing codes. Remarkably, even with this high rate, the performance of these codes remains comparable to that of conventional low-rate codes. This breakthrough opens up new possibilities for the realization of fault-tolerant quantum computers and the advancement of quantum computing technologies in the future.
The introduction of many-hypercube codes represents a significant advancement in the field of quantum error correction, offering a promising solution to the scalability challenges faced by traditional methods. By leveraging the elegant geometry and innovative decoder design of these codes, researchers like Hayato Goto are paving the way for more efficient and reliable quantum computing systems.
Leave a Reply